INTRODUCTION
I currently teach twenty-eight third graders at a small public school in Venice, California. It’s a vibrant school that has a very diverse school community. Recently big technology companies have been moving into the area, such as Google and Snapchat to name a few, adding an influx of international students to our rosters as their families relocate to work for these companies. I have the English Learners (ELs) in my class, five ELs and three students who have reclassified as fluent in English. Almost a third of my students are not native English speakers their first languages are French, Arabic, Japanese, Swedish, or Spanish. My class loves math time. It’s never quiet, it is abuzz with excitement as all my students are curious problem solvers who enjoy working together and sharing their ideas about different ways to attack math problems no matter their level of English proficiency.
They playfully improvise and share theories and findings, they change their work, they try a friend’s strategy. I watch a lot of mental math happen that never makes it onto the page. I provide time in math for students to discuss and record their thinking during the actual problem-solving portion of the lesson. Students model the problems in a variety of ways and record their solutions often very haphazard. I ask students to show different strategies, describe how they solved, and do a reflection on the lesson either as an exit ticket or for homework. Usually only five or six students ever take more than a few minutes to write about how they arrived at their solution or reflect on the day’s work. The metacognition involved in recording their thinking and reflecting on their learning is a critical part of the math lesson. The process of going deeper into their work as they follow their thinking is what I want them to discover and document.
As I examined their work, I noticed a disparity between how accurately they solve a problem when they collaborate compared to when the work independently. I gave an untimed interim math assessment and I was surprised by which students were ‘stuck’ and took an extraordinary amount of time to complete the fourteen questions. The results were comparable to the other third grade classes, 1/3 of the class below benchmark and 2/3 at or above benchmark, but some of my students who are the most productive and accurate struggled with the district assessment. I devised an assessment of my own to gauge the differences in working alone versus working collaboratively.
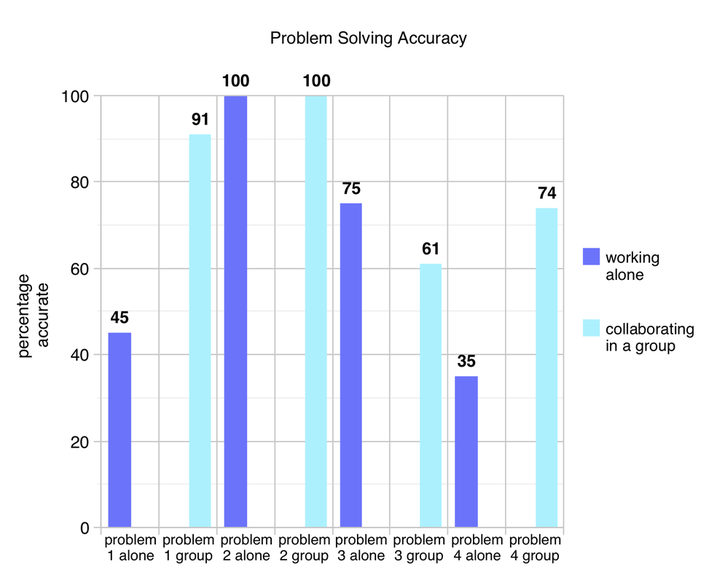
For my personal assessment, I gave a problem a day and told my students to show their work, as they do every day, only they may not talk or look at anyone else’s paper. I read the problem twice before they began. I didn’t unpack the problem or clarify anything. When they had completed the problem turned their paper over and read a book until everyone had completed the problem. We didn’t discuss the problems or talk about solutions as we usually would have done. The four questions covered the following skills: 3-digit subtraction, a multi-step problem using multiplication and subtraction, multiplication, and fractions. The next week I changed the phrasing of the problems and gave them essentially the same number sets. I read each question in the packet twice, and then let them solve all four problems together. Only one student noticed it was like the problems they had done the previous week. The results showed that working alone on the four problems they were 64% accurate and working in a collaborative group they were 82% accurate. (Table 1)
Table 1
They playfully improvise and share theories and findings, they change their work, they try a friend’s strategy. I watch a lot of mental math happen that never makes it onto the page. I provide time in math for students to discuss and record their thinking during the actual problem-solving portion of the lesson. Students model the problems in a variety of ways and record their solutions often very haphazard. I ask students to show different strategies, describe how they solved, and do a reflection on the lesson either as an exit ticket or for homework. Usually only five or six students ever take more than a few minutes to write about how they arrived at their solution or reflect on the day’s work. The metacognition involved in recording their thinking and reflecting on their learning is a critical part of the math lesson. The process of going deeper into their work as they follow their thinking is what I want them to discover and document.
As I examined their work, I noticed a disparity between how accurately they solve a problem when they collaborate compared to when the work independently. I gave an untimed interim math assessment and I was surprised by which students were ‘stuck’ and took an extraordinary amount of time to complete the fourteen questions. The results were comparable to the other third grade classes, 1/3 of the class below benchmark and 2/3 at or above benchmark, but some of my students who are the most productive and accurate struggled with the district assessment. I devised an assessment of my own to gauge the differences in working alone versus working collaboratively.
For my personal assessment, I gave a problem a day and told my students to show their work, as they do every day, only they may not talk or look at anyone else’s paper. I read the problem twice before they began. I didn’t unpack the problem or clarify anything. When they had completed the problem turned their paper over and read a book until everyone had completed the problem. We didn’t discuss the problems or talk about solutions as we usually would have done. The four questions covered the following skills: 3-digit subtraction, a multi-step problem using multiplication and subtraction, multiplication, and fractions. The next week I changed the phrasing of the problems and gave them essentially the same number sets. I read each question in the packet twice, and then let them solve all four problems together. Only one student noticed it was like the problems they had done the previous week. The results showed that working alone on the four problems they were 64% accurate and working in a collaborative group they were 82% accurate. (Table 1)
Table 1
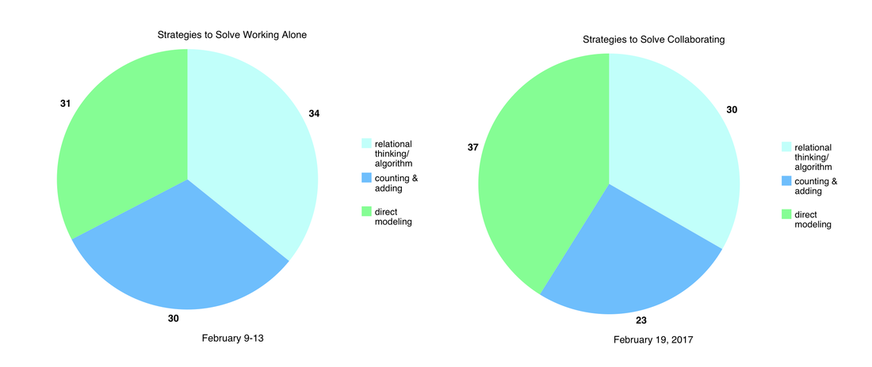
There is also a difference in what strategies they use to work out the problem. Students will typically solve a problem by using one or more of three strategies. The typical categories for problem-solving strategies are: direct modeling being the most concrete as students represent each object, to counting and adding where students are showing each group or part of the problem using numbers, to solving using relational thinking including the standard algorithm. My goal is to have my students begin to move away from direct modeling towards relational thinking, but as you can see from the results, about a third of my students use each strategy whether they are working alone or together. I know that two of the skills, fractions and regrouping in larger digit subtraction, are new so it is was not surprising to see so much direct modeling. (Table 2.) I would like to see a progression in accuracy and number sense through the development of my math curriculum.
Table 2.
Table 2.
I would like to explore more ways to make their learning visible and have them reflect on their learning. The metacognition involved in recalling what they learned, visually representing their thoughts, and sharing their thinking should result in being able to recall content. I’d like to give my students a broader written vocabulary and visual vocabulary in which to explore content. Through sketchnoting and graphic recording lessons in conjunction with resources on cognitively guided instruction, I would like to help my students make sense of their thoughts by making their learning and thinking more visible.
RQ: How does having students document their mathematical thinking visually help them achieve understanding and master the content?
Subquestion: How does having students record all aspects of their mathematical thinking in a math lesson inform my teaching?
RQ: How does having students document their mathematical thinking visually help them achieve understanding and master the content?
Subquestion: How does having students record all aspects of their mathematical thinking in a math lesson inform my teaching?